

But now, our sentence has two parts that are atomic sentences, P and Q.
#Geometry symbols p q conditional how to
We know how to write the conditional, but what does it mean? As before, we will take the meaning to be given by the truth conditions-that is, a description of when the sentence is either true or false.
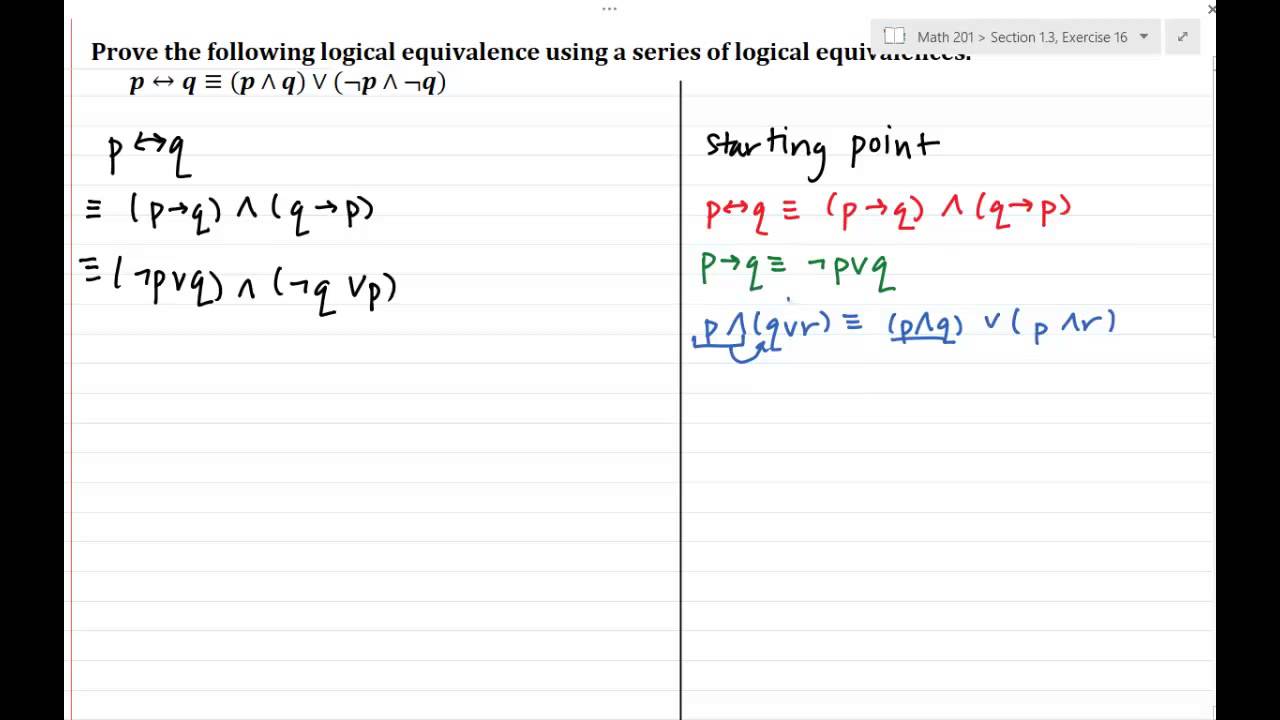
The second sentence (the one after the arrow, which in this example is “ Q”) is called the “consequent”. The first constituent sentence (the one before the arrow, which in this example is “ P”) is called the “antecedent”. It is also sometimes called a “material conditional”. This kind of sentence is called a “conditional”. There are several ways to do this, but the most familiar (although not the most elegant) is to use parentheses. In that case, we need a way to identify that this is a single sentence when it is combined with other sentences. We might want to combine this complex sentence with other sentences. One last thing needs to be observed, however. The most commonly used such symbol is “→”. It will be useful, however, to replace the English phrase “if…then…” by a single symbol in our language. Then, the whole expression could be represented by writing We could thus represent this sentence by lettingīe represented in our logical language by The sentence, “If Lincoln wins the election, then Lincoln will be President” contains two atomic sentences, “Lincoln wins the election” and “Lincoln will be President”. Thus, it would be useful if our logical language was able to express these kinds of sentences in a way that made these elements explicit. To make these relations explicit, we will have to understand what “if…then…” and “not” mean. And the second sentence above will, one supposes, have an interesting relationship to the sentence, “The Earth is the center of the universe”. For example, the first sentence tells us something about the relationship between the atomic sentences “Lincoln wins the election” and “Lincoln will be President”. We could treat these like atomic sentences, but then we would lose a great deal of important information. The Earth is not the center of the universe. If Lincoln wins the election, then Lincoln will be President. “If…then….” and “It is not the case that….” 2.1 The ConditionalĪs we noted in chapter 1, there are sentences of a natural language, like English, that are not atomic sentences. In the last two cases, your friend didn’t say anything about what would happen if you didn’t upload the picture, so you can’t say that their statement was wrong.2. There is only one possible case in which you can say your friend was wrong: the second outcome in which you upload the picture but still keep your job.


The website never said that paying for expedited shipping was the only way to receive the jersey by Friday.Ī friend tells you “If you upload that picture to Facebook, you’ll lose your job.” Under what conditions can you say that your friend was wrong?ġ) You upload the picture and lose your jobĢ) You upload the picture and don’t lose your jobģ) You don’t upload the picture and lose your jobĤ) You don’t upload the picture and don’t lose your job Remember, though, that if the antecedent is false, we cannot make any judgment about the consequent. It may seem strange that the third outcome in the previous example, in which the first part is false but the second part is true, is not a lie. The fourth outcome is not a lie because, again, the website didn’t make any promises about when the jersey would arrive if you didn’t pay for expedited shipping. The third outcome is not a lie because the website never said what would happen if you didn’t pay for expedited shipping maybe the jersey would arrive by Friday whether you paid for expedited shipping or not. The first outcome is exactly what was promised, so there’s no problem with that. Only one of these outcomes proves that the website was lying: the second outcome in which you pay for expedited shipping but don’t receive the jersey by Friday. In what situation is the website telling a lie?ġ) You pay for expedited shipping and receive the jersey by FridayĢ) You pay for expedited shipping and don’t receive the jersey by Fridayģ) You don’t pay for expedited shipping and receive the jersey by FridayĤ) You don’t pay for expedited shipping and don’t receive the jersey by Friday The website says that if you pay for expedited shipping, you will receive the jersey by Friday. Suppose you order a team jersey online on Tuesday and want to receive it by Friday so you can wear it to Saturday’s game. TFF is the only scenario in which Anaheim will make the playoffs. To illustrate this situation, suppose that Anaheim will make the playoffs if: (1) Anaheim wins, and (2) neither Boston nor Cleveland wins. It turns out that this complex expression is true in only one case: when A is true, B is false, and C is false.


 0 kommentar(er)
0 kommentar(er)
